Inégalités de BienayméTchebychev et de concentration Mathématiques Explication et Exercices

On propose trois démonstrations de l’inégalité de Bienaymé-Tchebychev. La démonstration moderne telle qu’on pourrait l’enseigner en L3. On verra pourquoi elle n’est sans doute pas utilisable en terminale. Une démonstration niveau Terminale qui s’inspire du texte initial de Bienaymé (1853), avec des notations plus lisibles de.. En théorie des probabilités, l’ inégalité de Bienaymé-Tchebychev, est une inégalité de concentration permettant de montrer qu’une variable aléatoire prendra avec une faible probabilité une valeur relativement lointaine de son espérance. Ce résultat s’applique dans des cas très divers, nécessitant la connaissance de peu de.

Practique el uso de la desigualdad de Chebyshev

INEGALITE DE BIENAYME TCHEBYCHEV YouTube

Inégalité de Tchebychev part1 YouTube

Inégalité de Tchebychev [AlgAB19] YouTube

Inégalités de Markov et de BienayméTchebytchev application à la loi géométrique YouTube

TD18 Ex15 Inégalité de Bienaymé Tchebychev YouTube

Cours maths terminale Inégalités de Markov et de BienayméTchebychev

L’inégalité de BienayméTchebychev YouTube

Variables aléatoires/Inégalité de BienayméTchebichev PCSI 2 Séance 101 Chapitre 26 Variables

INEGALITE DE MARKOV. DÉMONSTRATION YouTube

INÉGALITÉ DE BIENAYMÉTCHEBYCHEV. TERMINALE YouTube

inégalité de bienaymé tchebychev scilab

Inégalité de Tchebychev —

Comment appliquer l’inégalité de BienayméTchebychev ? YouTube

Inégalités de BienayméTchebychev et de concentration Mathématiques Explication et Exercices

l’inégalité de bienaymé tchebychev

L’intuition derrière l’inégalité de Tchebychev et la loi des grands nombres YouTube

[POST BAC] Inégalités de Markov et de Bienaymé Tchebychev (Maths) YouTube

L3GC vidéo 5.1 Inégalité de Bienaymé Tchebychev (BAT) YouTube

Inégalité de Tchebychev Les Sup1jectifs YouTube

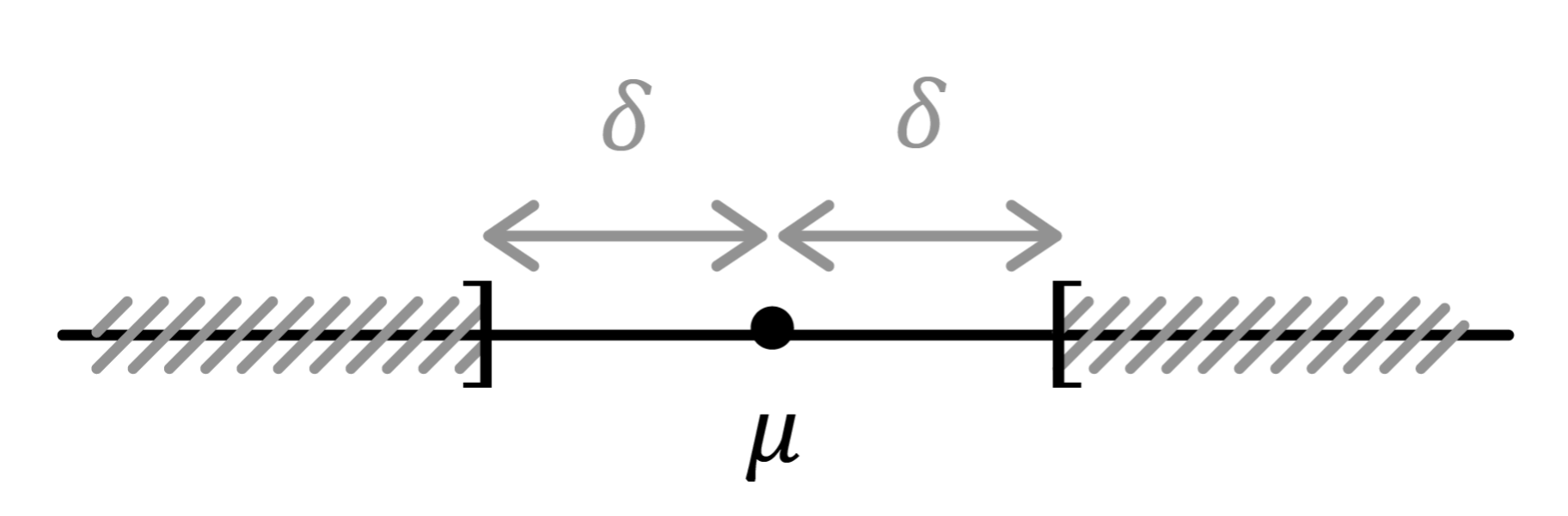
L’inégalité de Bienaymé-Tchebychev et toutes les inégalités de concentration apportent des précisions sur cette dispersion. Si X est une variable aléatoire à valeurs positives et si E(X) E X désigne son espérance, alors, pour tout réel a a strictement positif : P(X ≥ a) ≤ E(X) a P X ≥ a ≤ E X a. En notant μ μ l.. Propriété. Cette inégalité fut découverte par Bienaymé en 1856 puis popularisée par Tchebychev, grâce à l’utilisation de la loi des grands nombres. Soit X une variable aléatoire admettant comme espérance mu et comme variance V, Pour tout Ɛ > 0, on a : P (|X – mu |) ≥ Ɛ ≤ V/Ɛ 2.