Cálculo 3. Coordenadas cilíndricas y esféricas en integrales triples

Convierta las coordenadas rectangulares (−1, 1, √6) en coordenadas esféricas y cilíndricas. Solución: Comience convirtiendo de coordenadas rectangulares a esféricas: Como ( x, y) = (- 1, 1), la elección correcta para θ es 3π/4. En realidad, hay dos formas de identificar φ. Podemos usar la ecuación.. r = ρ Uρ + 0 Uφ + z Uz. Por otra parte, un desplazamiento infinitesimal dr a partir del punto P se expresa de la siguiente manera:. d r = dρ Uρ + ρ dφ Uφ + dz Uz. De forma similar, un elemento infinitesimal de volumen dV en coordenadas cilíndricas es:. dV = ρ dρ dφ dz. Ejemplos. Hay infinidad de ejemplos del uso y aplicación de las coordenadas cilíndricas.

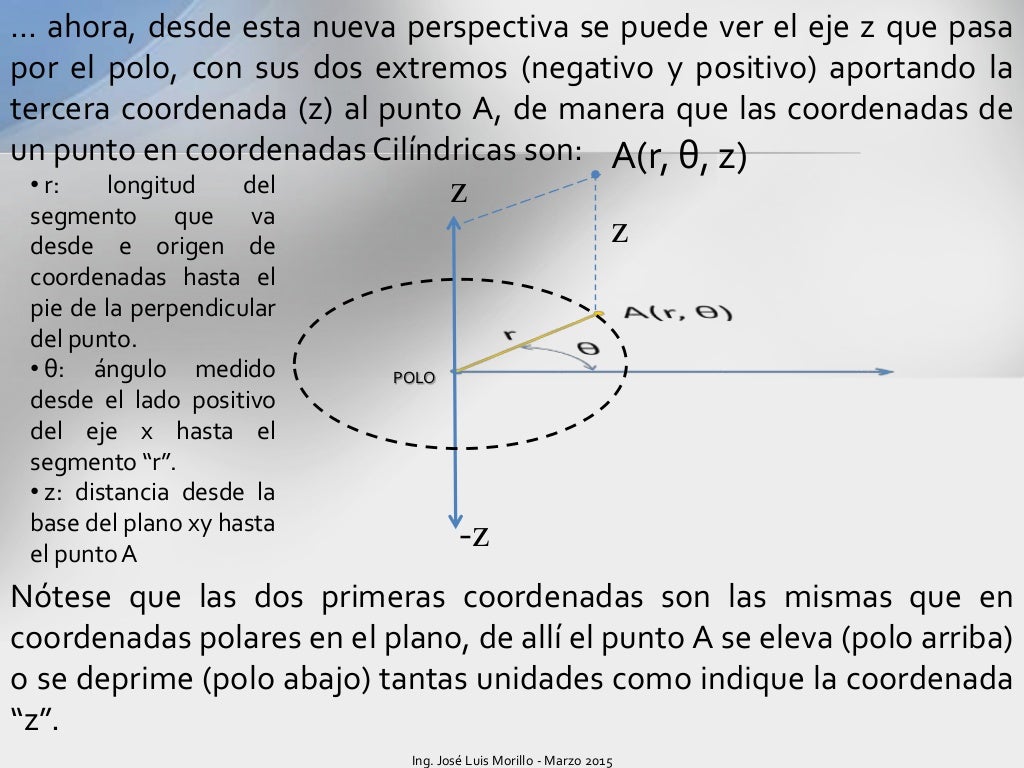
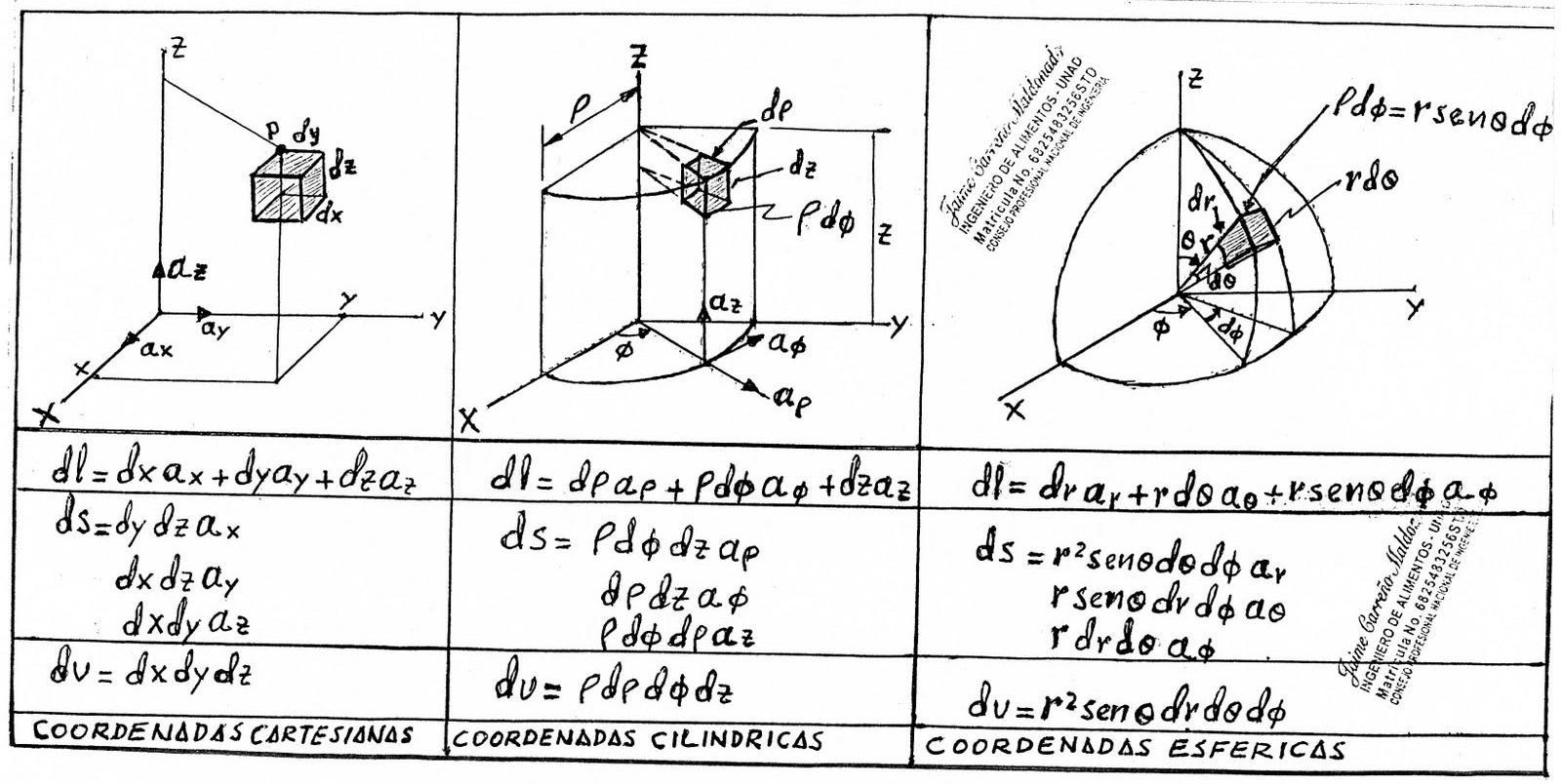
Coordenadas cilindricas y esfericas

Vectores unitarios en el sistema de coordenadas cilíndrico en función

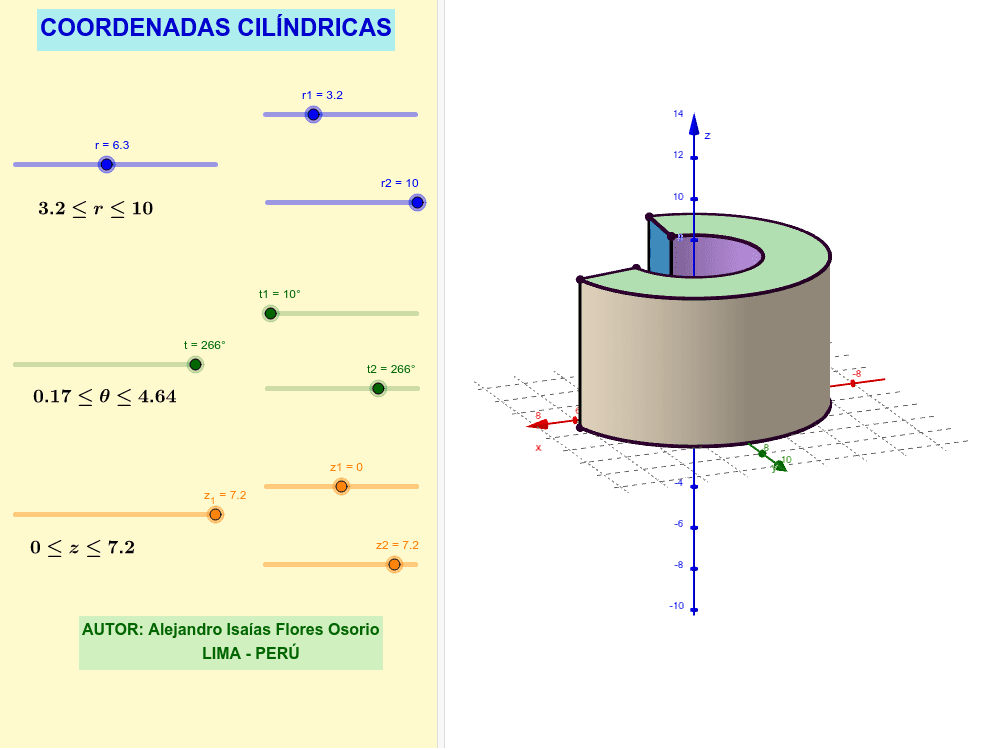
Coordenadas Cilíndricas GeoGebra

Coordenadas Esféricas Convertir coordenadas cartesianas a coordenadas

Coordenadas Cilíndricas Convertir coordenadas cartesianas a

Transformación de coordenadas esféricas y cilíndricas YouTube

coordenadas cilindricas e esfericas Geometria Analítica

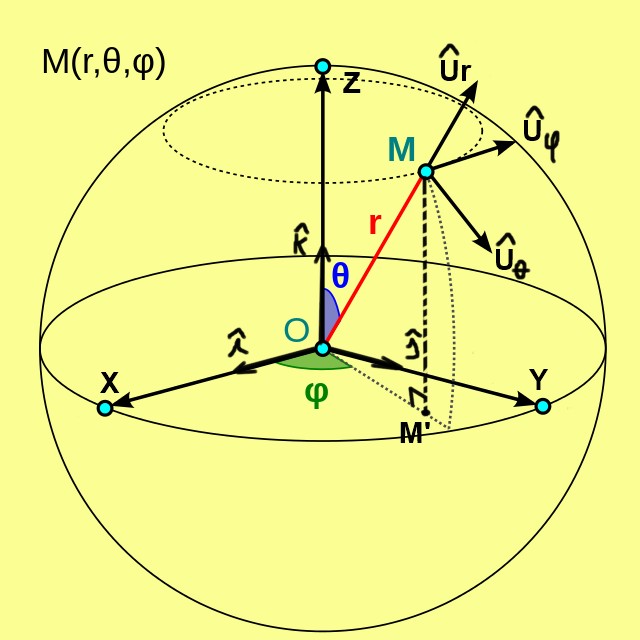
Coordenadas esféricas ejemplos y ejercicios resueltos

Calaméo Coordenadas Cilindricas Y Esfericas

Coordenadas Cilindricas e Esferica

Coordenadas cilindricas y esfericas [PDF Document]

Introducción Coordenadas Cilíndricas YouTube

Coordenadas cilíndricas y esféricas YouTube

Coordenadas Cilíndricas YouTube

Coordenadas Cilindricas y Esfericas 12 PDF Sistema coordinado Esfera

CONVERSIÓN DE COORDENADAS Rectangulares, cilíndricas y esféricas

Ejemplo convertir un vector dado en coordenadas esféricas a cartesianas

16 Coordenadas cilíndricas y esféricas YouTube

Usando Coordenadas Cilíndricas Para Calcular Integrais Triplas? YouTube

Parametrización de la esfera con coordenadas esféricas YouTube

Los sistemas de coordenadas cartesianos, ya sea en 2D o en 3D, son los más utilizados. Pero en algunas ocasiones nos puede convenir usar otro tipo de sistema de coordenadas. El sistema de coordenadas polares es un sistema de referencia bidimensional cuyas coordenadas son: es la distancia entre el origen de coordenadas y el punto.. Recordemos que para convertir de coordenadas cartesianas a cilíndricas, podemos usar las siguientes ecuaciones: ( θ)) = 4. Recordemos eso cos2(θ) +sin2(θ) = 1 cos 2. ( θ) = 1. Así r2 = 4 r 2 = 4 o r = 2 r = 2. Las coordenadas esféricas y cilíndricas son dos generalizaciones de coordenadas polares a tres dimensiones.