地理院地図では、土地の断面図を簡単に作成できます。. また、高さを色分けした地図（陰影起伏図・デジタル標高地形図）や「3D」機能で、土地の高低差を視覚的に理解することができます。. – 目 次 -. 地図から高さを知る（断面図・マウスオーバー.. Google Earth プロを起動します。 パスを描くか、既存のパスを開きます。 [編集] [高度プロファイルを表示] をクリックします。3D ビューアの下部に高度プロファイルが表示されます。高度測定値が「0」である場合は、地形レイヤが有効になっていることを確認します。
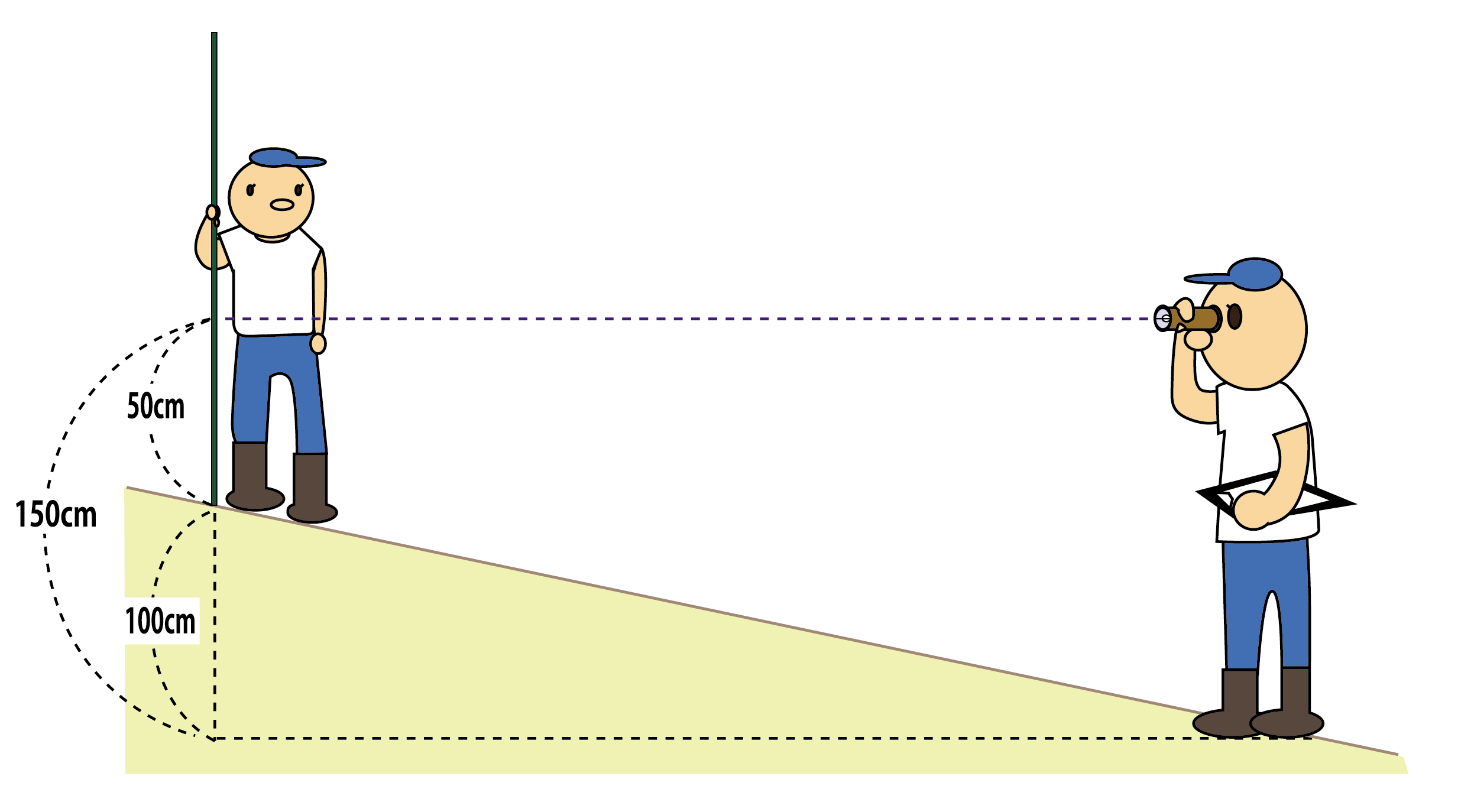
マルドリ設計支援システム 高低差測量
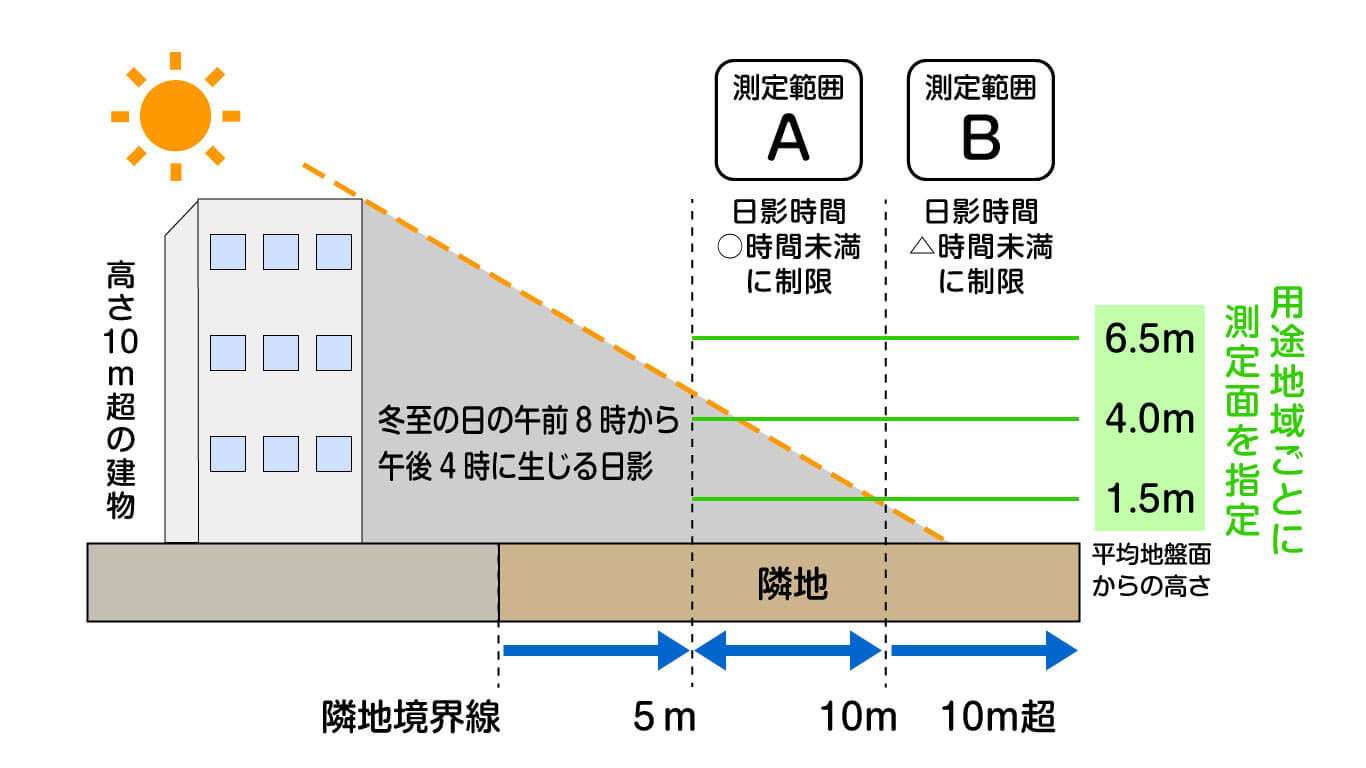
我が家の天井は何故斜め？良好な生活環境を守るための建物の高さ制限とは？ TOKYO 14区
デリカD5 in 北海道 木の高さ
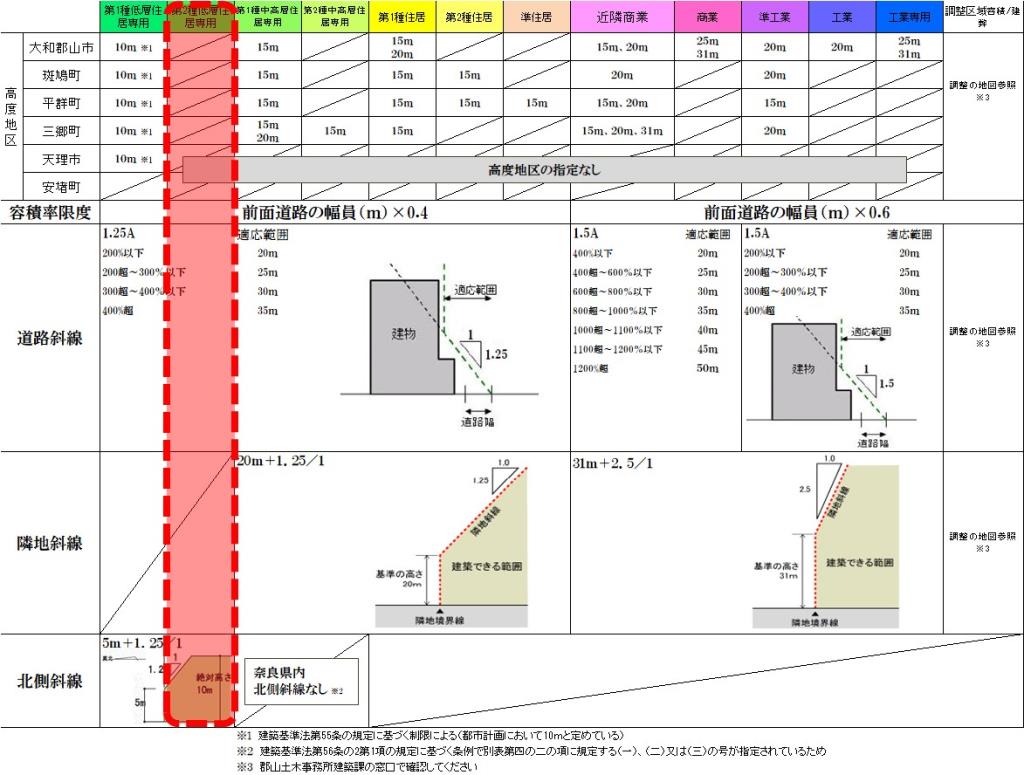
建築基準法に基づく建築物の高さ等の制限について/奈良県公式ホームページ
スタッフの読み方（レベルで高さを測る） YouTube
3C数学、相似を利用して校舎の高さを測定しました。 東海大学付属大阪仰星高等学校中等部・高等学校
一瞬で距離を測定できる！面積・容積・高さが計測できるレーザー距離計を10月7日発売 Japan
iPhoneを使って、ビルや山などの高さを測る方法 順番学研究所
小6【縮図の利用】「実際の木の高さ」 ノートに書こう！ YouTube
モノづくり大好き監督から届く、建築現場ブログ 高さを測る機械
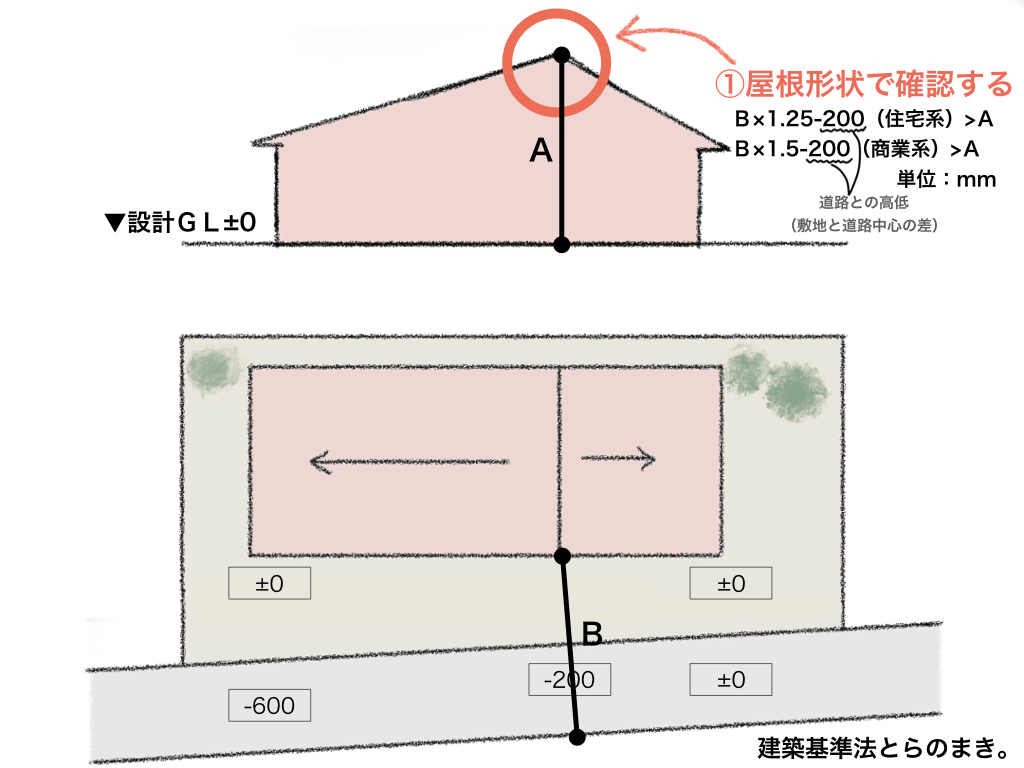
8ACFFF75CE5C44DFA6CEC372DC5DE052｜建築基準法とらのまき。
和算の問題【木の高さを測る】解答編 レオん家【関西発の教育ブログ】
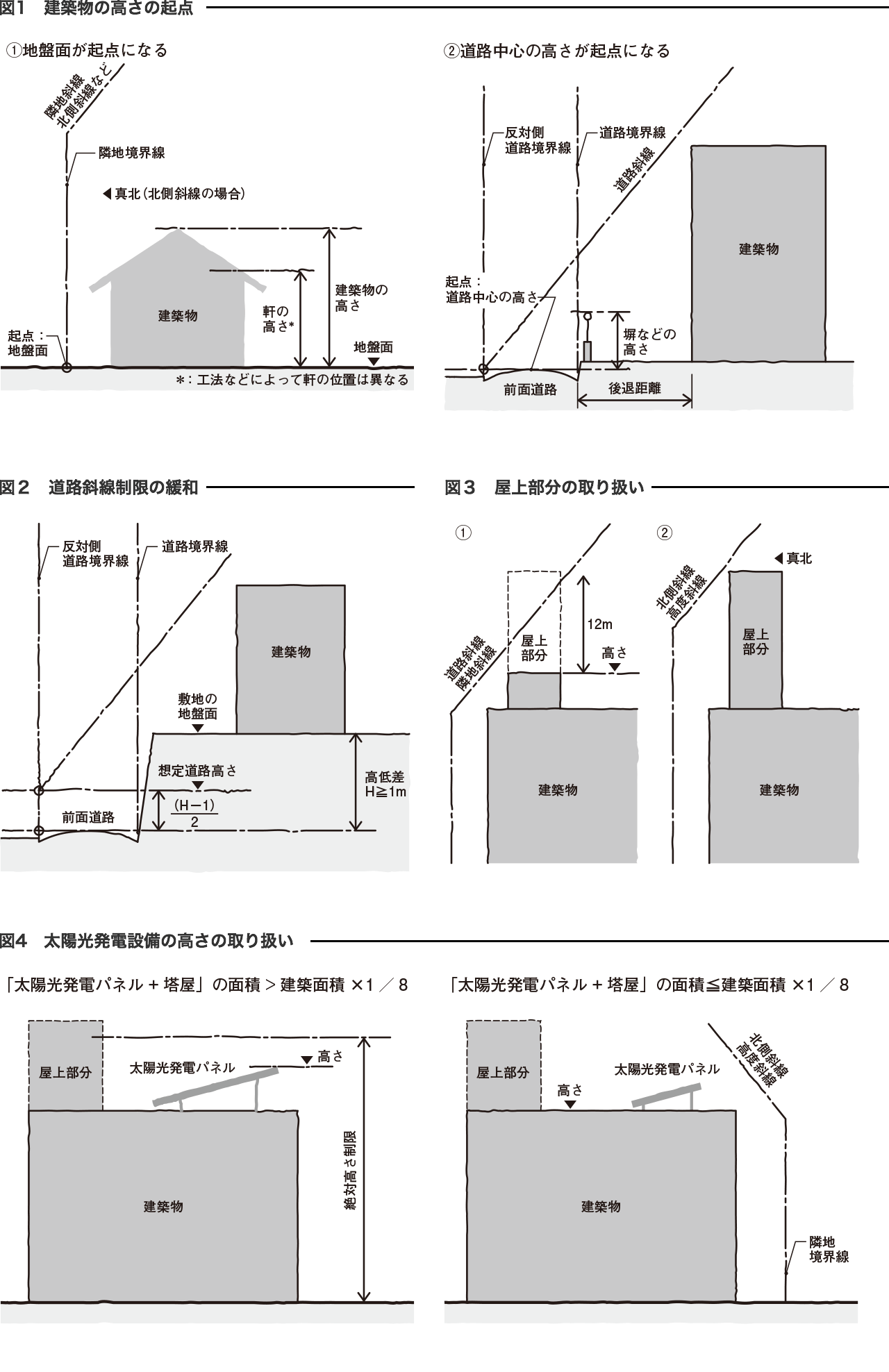
第6回 建築基準法 集団規定マスターへの道 高さ① 建築設計研究所
測量について
高さ測定器 安全・簡単・正確に高さが測定出来ます。
実在する建物や敷地の長さを測れる方法『グーグルアース』 YouTube
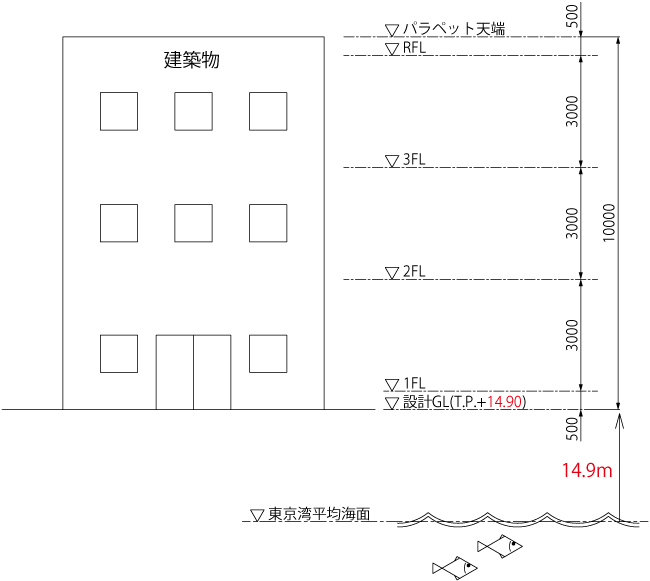
建築物の高さの基準 ワンポイント情報 カネソウ株式会社 建設用金属製品の総合メーカー
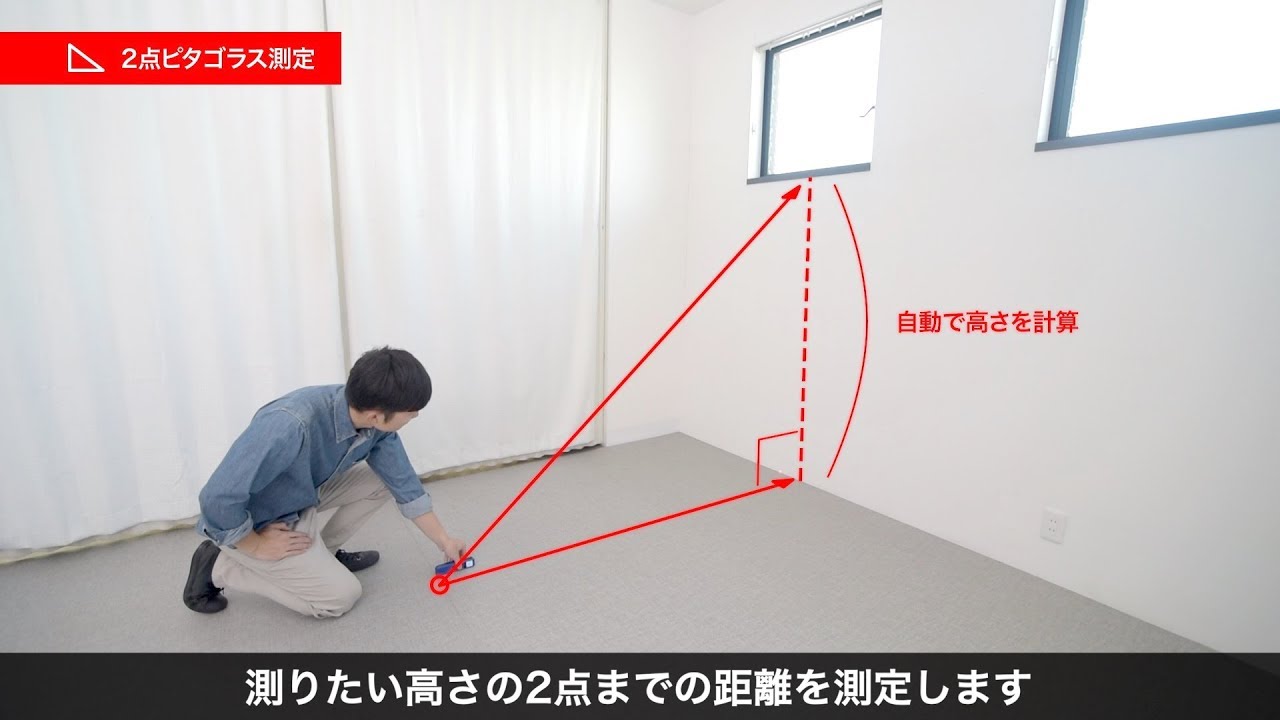
レーザー距離計（最大測定距離40m・尺単位対応・面積/体積/ピタゴラス計測対応）400TST009 YouTube
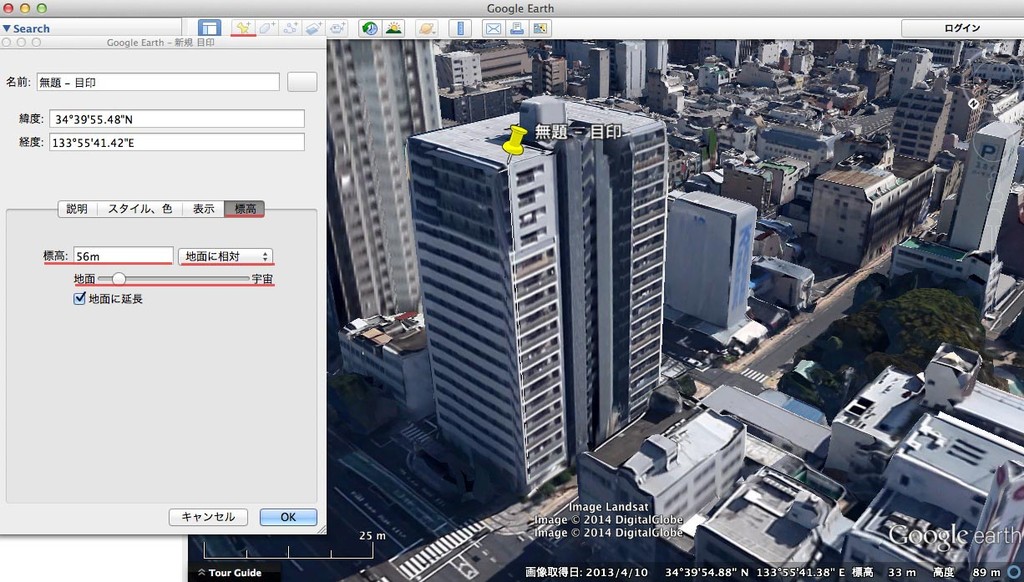
模型屋と3DCAD Google Earthで高さを測る
天井高さの基準とは｜平均天井高さの求め方も解説【法施行令21条】 確認申請ナビ
お手軽な方法ですとビルの一階の部分の高さをメジャーを伸ばして計ってそれを階数分だけ掛ければだいたいの高さが出せます。 もっと簡単に出したい場合にはビルの一階分の高さというのはだいたい3.5mぐらいですから階数×3.5で高さが出てきます。. この建物の高さを計るために12m離れた地点から高さを計測しました。 視点の高さ1.7mからみたときに、仰角は30°でした。このときの建物の高さを求めてみましょう。 、 、 とします。 まず、三角形ABCについてみてみましょう。
